문제
https://www.acmicpc.net/problem/2211
풀이
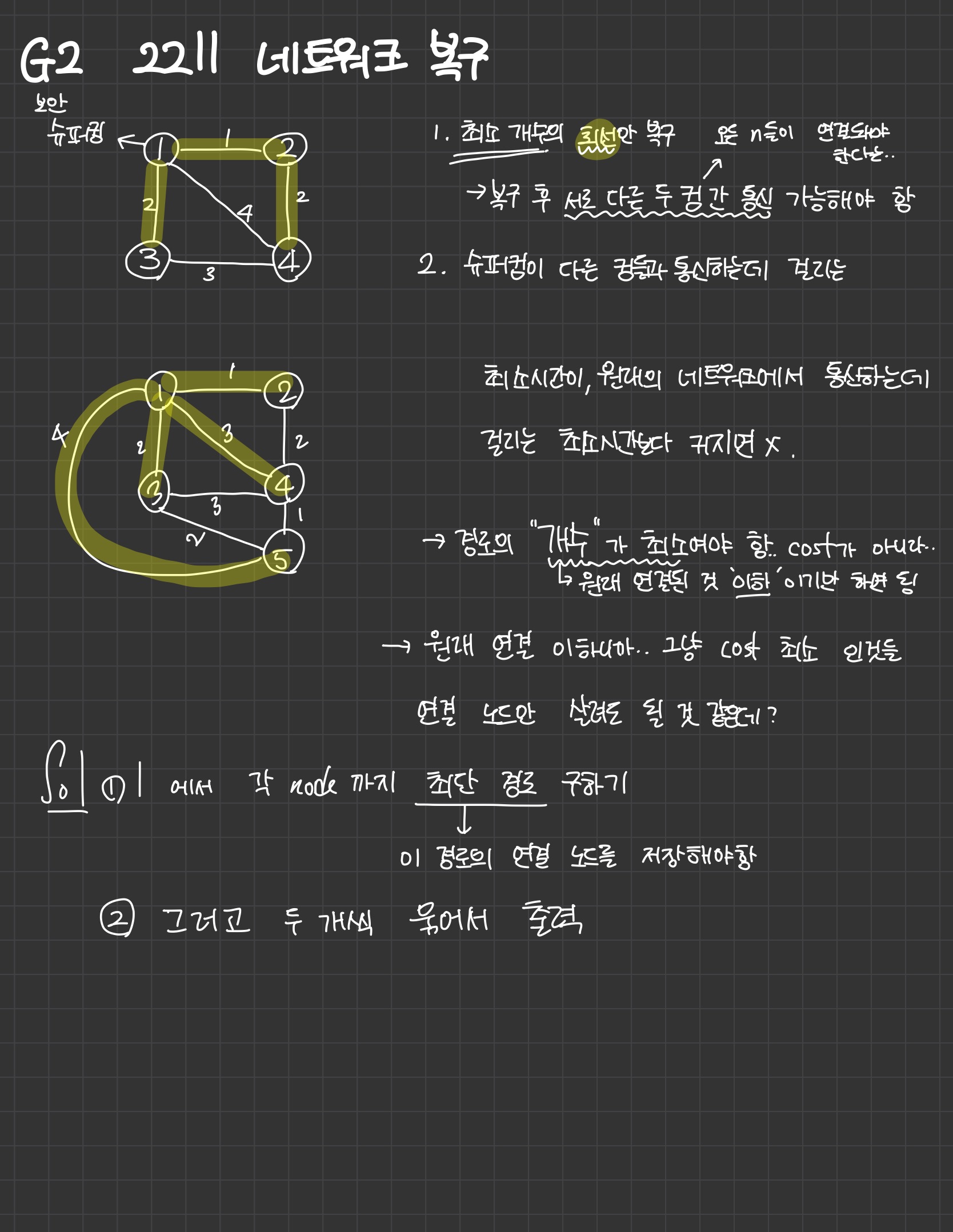
1. 1번 컴퓨터에서 각각의 컴퓨터까지 다익스트라를 이용해 최단 경로 구하기
-> 이 부분에서 처음에 문제를 읽고 '경루의 개수가 최소여야한다'는 말 때문에 헷갈렸으나, 원래 연결된 경로에서의 최소 시간 보다 크면 안된다는 말, 즉 최소 cost를 그대로 유지해야 한다는 말이 추가로 있기 때문에, 다익스트라로 최소 비용이 드는 루트들만 남기면 되는거였다.
2. 이때 1번 컴퓨터에서 각 노드까지의 루트를 저장해둔다.
-> 2차원 배열 route를 사용하여 저장해줬다.
3. 2에서 저장해둔 루트를 중복 없이 출력한다.
-> route 배열을 2중 for문으로 돌며 중복을 없애기 위해 pair자료형의 set인 finalRoute에 넣어줬다.
코드
//2211 네트워크 복구
#include <iostream>
#include <queue>
#include <vector>
#include <set>
#define INF 1e9
using namespace std;
int n, m;
vector<pair<int, int>> graph[1001];
int dist[1001];
vector<int> route[1001]; //route[3] = {1, 4, 3} 이면 1->3의 최소비용 경로는 1->4->3
set<pair<int, int>> finalRoute; //정점을 두개씩 묶되 중복처리를 위해 pair자료형의 set 사용
void dijkstra(){
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, 1});
dist[1] = 0;
route[1].push_back(1);
while (!pq.empty()){
auto [cost, curr] = pq.top();
pq.pop();
for(long unsigned int i = 0; i< graph[curr].size(); i++){
auto [next, nextCost] = graph[curr][i];
if(dist[next] <= cost + nextCost) continue;
dist[next] = cost + nextCost;
pq.push({dist[next], next});
//다익스트라의 cost를 갱신할때마다 route를 저장(이전루트 + next 노드)
route[next] = route[curr];
route[next].push_back(next);
}
}
}
int main(){
cin >> n >>m;
for(int i = 0; i<m; i++){
int a, b, cost;
cin >> a >> b>> cost;
graph[a].push_back({b, cost});
graph[b].push_back({a, cost});
}
fill_n(dist, n + 1, INF);
dijkstra();
//route 배열에 있는 정점들을 두개씩 묶어 finalRoute set에 pair로 저장
for(int i = 1 ; i<= n; i++){
for(long unsigned int j = 0; j < route[i].size()-1 ; j++){
finalRoute.insert({route[i][j], route[i][j+1]});
}
}
cout << finalRoute.size() <<"\n";
//finalRoute에 있는 간선들을 출력
for(set<pair<int, int>>::iterator it = finalRoute.begin(); it != finalRoute.end(); it++) {
cout << it->first <<" " << it->second<<"\n";
}
}
핵심
1. 양방향 그래프이므로 간선들을 입력받을 때 두 쪽에서 모두 추가해준다.
2. 다익스트라의 cost를 갱신할 때 경로가 달라진 것이기 때문에 route배열을 다시 초기화한다.
풀이흔적
처음에 이렇게 풀었다가 틀렸었다,,
#include <iostream>
#include <queue>
#include <vector>
#include <set>
#define INF 1e9
using namespace std;
int n, m;
vector<pair<int, int>> graph[1001];
int dist[1001];
set<int> route[1001]; //route를 vector가 아닌 set로 선언했음
set<pair<int, int>> finalRoute;
void dijkstra(){
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, 1});
dist[1] = 0;
route[1].insert(1);
while (!pq.empty()){
auto [cost, curr] = pq.top();
pq.pop();
for(long unsigned int i = 0; i< graph[curr].size(); i++){
auto [next, nextCost] = graph[curr][i];
if(dist[next] <= cost + nextCost) continue;
dist[next] = cost + nextCost;
pq.push({dist[next], next});
route[next] = route[curr];
route[next].insert(next);
}
}
}
int main(){
cin >> n >>m;
for(int i = 0; i<m; i++){
int a, b, cost;
cin >> a >> b>> cost;
graph[a].push_back({b, cost});
graph[b].push_back({a, cost});
}
fill_n(dist, n + 1, INF);
dijkstra();
//route가 set이므로 iterator를 써야했기에 조금 더 복잡해보이지만, 결론적으론 같은 처리를 해줌
for(int i = 1 ; i<= n; i++){
int size = route[i].size();
for(int j = 0; j < size - 1; j++){
set<int>::iterator it = route[i].begin();
finalRoute.insert({*it, *(++it)});
route[i].erase(route[i].begin());
}
}
cout << finalRoute.size() <<"\n";
for(set<pair<int, int>>::iterator it = finalRoute.begin(); it != finalRoute.end(); it++) {
cout << it->first <<" " << it->second<<"\n";
}
}
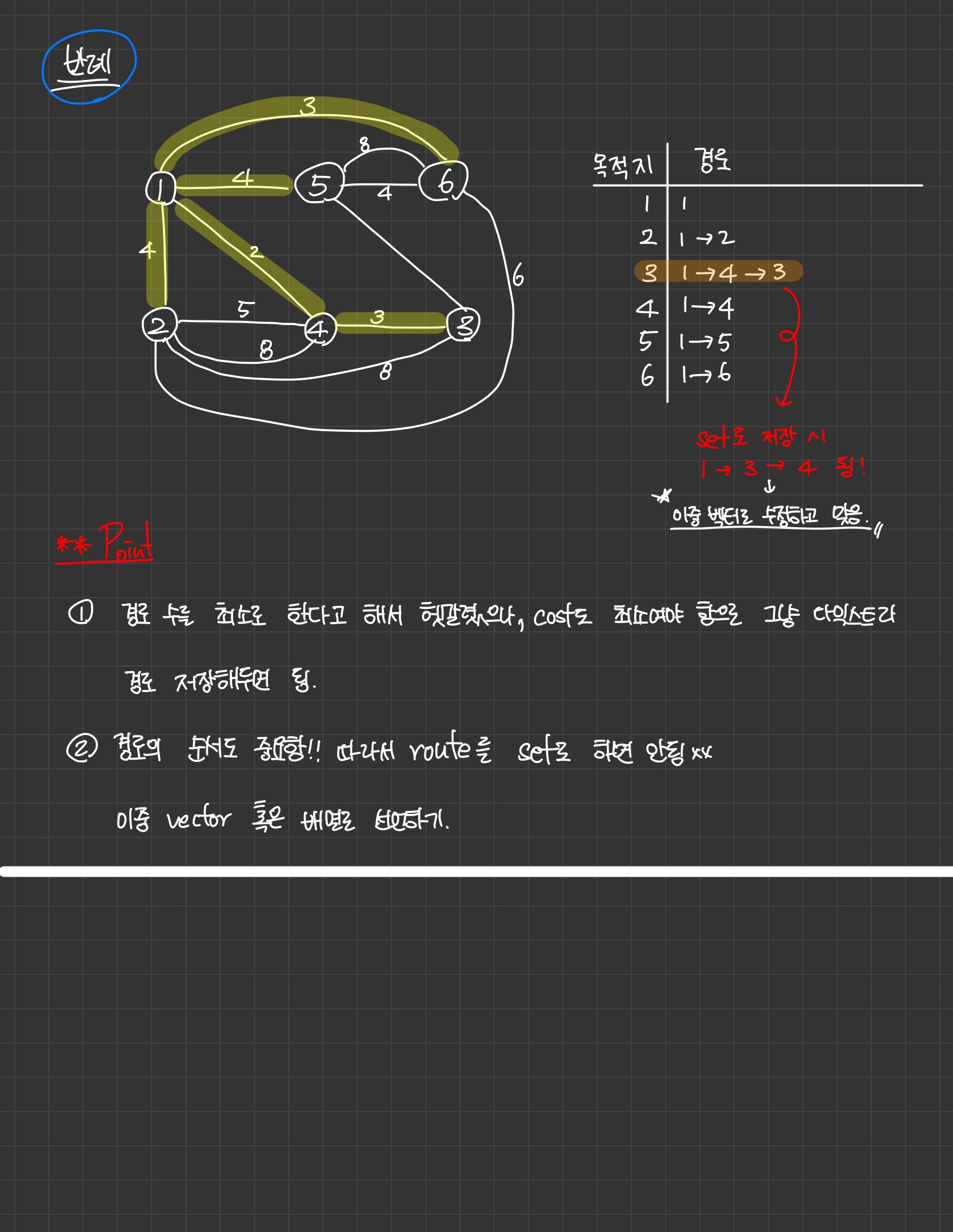
유일한 차이는 route를 2차원 배열(이중 벡터배열? 뭐라고 부르죠..)이 아닌 set 배열로 선언했던 것.
처음에 '중복 되지 않아야한다'는 거에 꽂혀서 set로 했었다.
일단 예제가 잘 돌아가길래 제출했는데 틀림

디버깅으로 하나하나 따라가봤는데도 잘 되는데 ㅠㅜ 왜 안되는겨,,
하면서 질문 게시판을 돌아다니며 반례 예제를 찾아봤다.
https://www.acmicpc.net/board/view/70830
그리고 위 글을 발견!!!!
써두신 예제를 돌려봤는데 틀리게 나왔다 ㅋ
다시 한번 디버깅을 해보니,
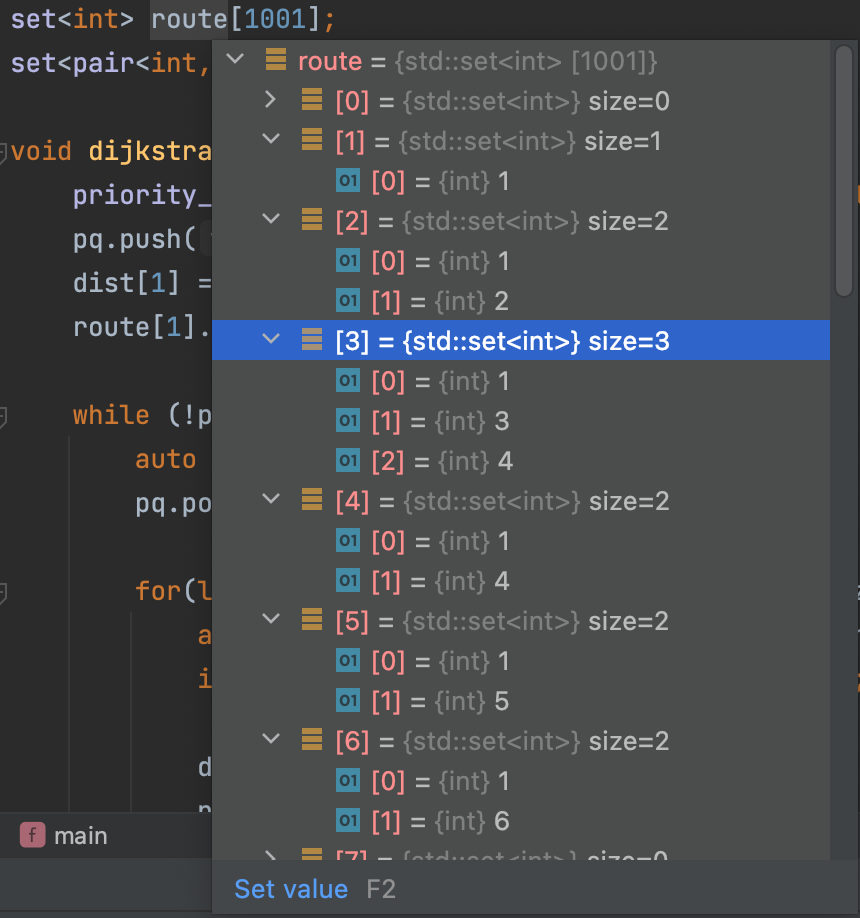
route를 set 배열로 선언했기 때문에,
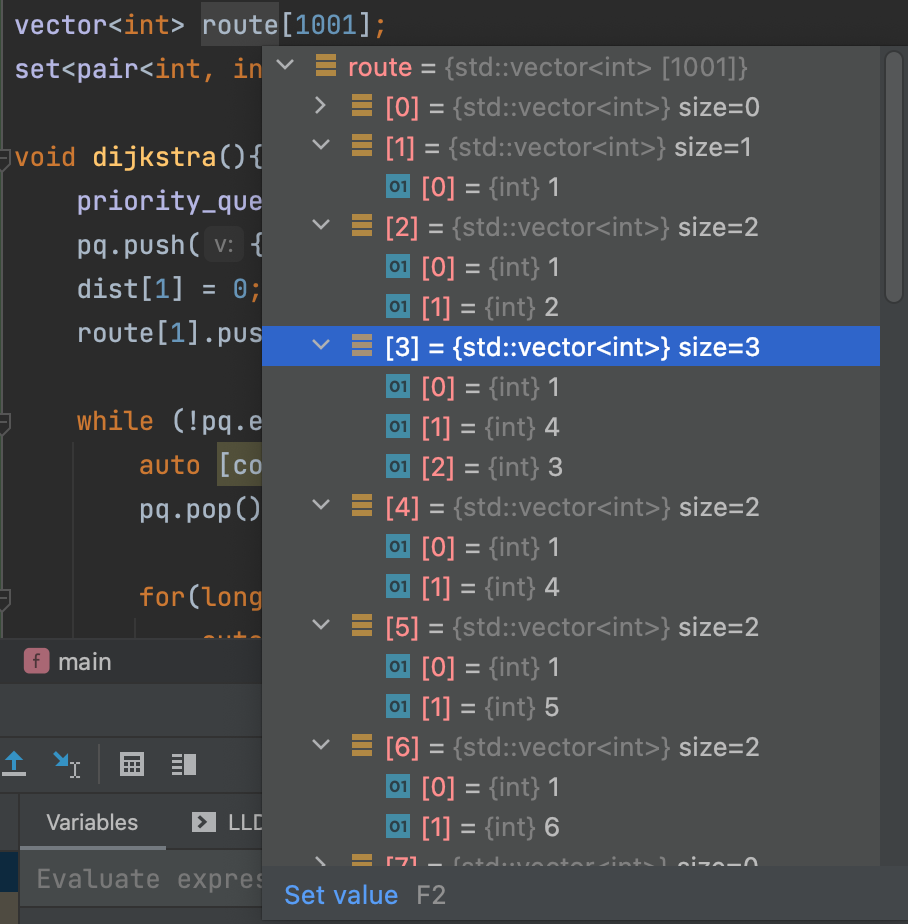
1에서 3번컴퓨터까지의 최소비용 경로가 1 -> 4 -> 3 인데
1 -> 3 -> 4 로 저장되고 있었다!
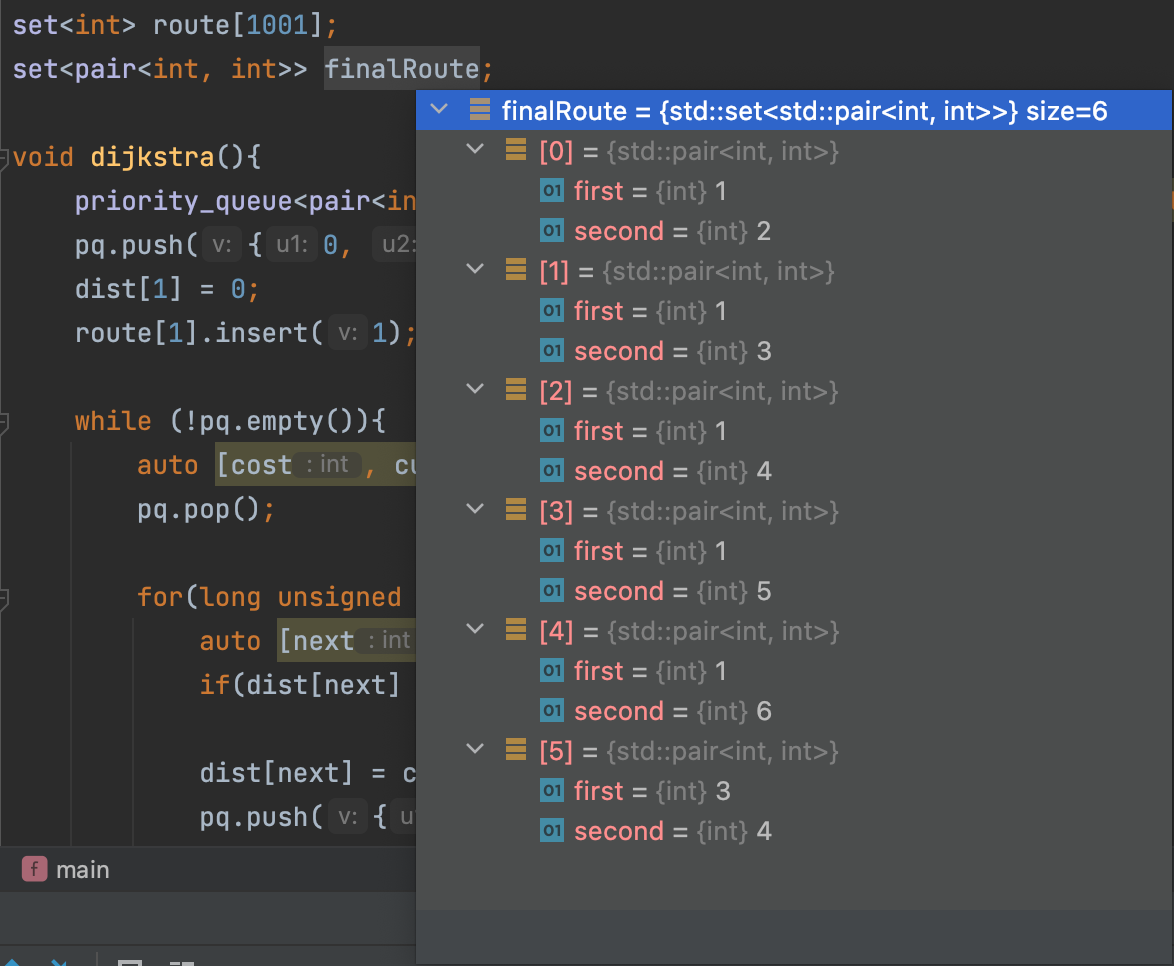
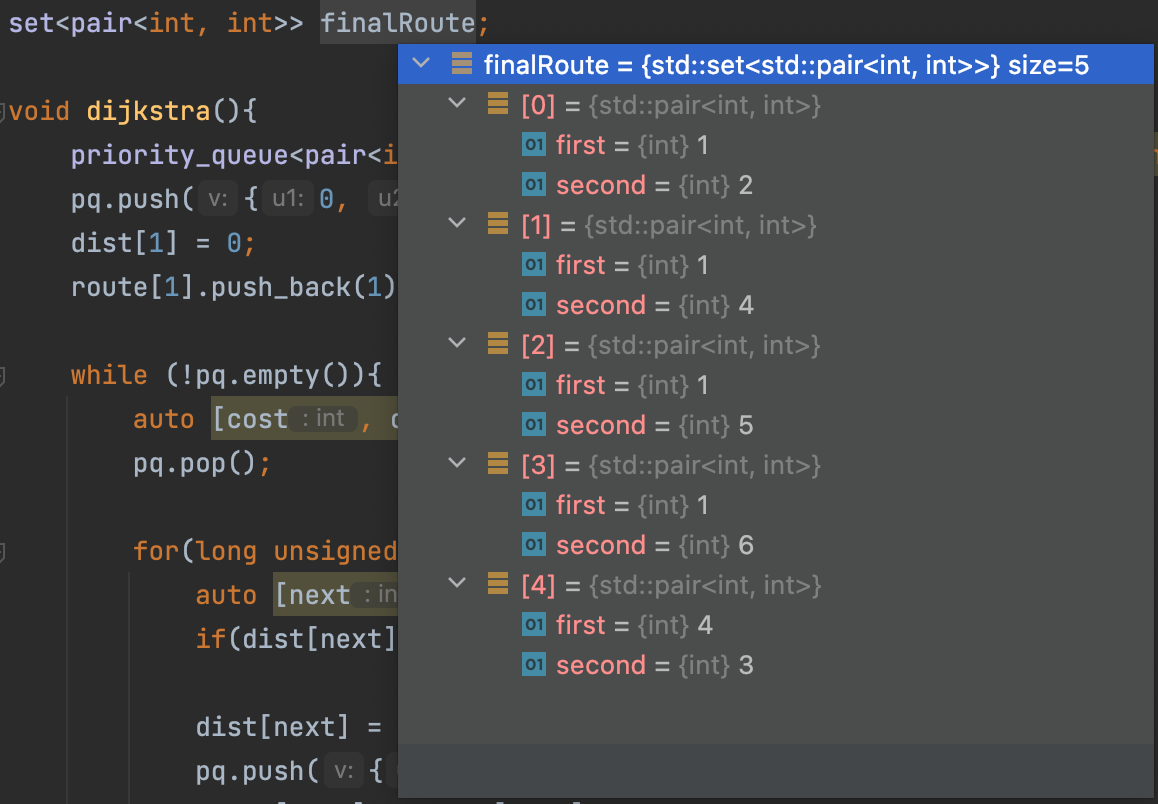
그래서 답도 다르게 출력되고 있던 것.
바로 route를 벡터 배열로 고쳤고, 맞았음!!!!
set 배열과 벡터 배열로 선언한 route의 저장값 비교 :
그 결과 각각 finalRoute 비교 :


풀이 흔적
'알고리즘' 카테고리의 다른 글
| [백준/BOJ] acmicpc 14938 서강그라운드 C++ (다익스트라) (0) | 2024.05.29 |
|---|---|
| [백준/BOJ] acmicpc 11799 최소비용 구하기2 C++ (다익스트라) (0) | 2024.05.29 |
| [백준] acmicpc 2446 별 찍기 9 C++ 풀이 (1) | 2023.11.21 |
| [백준 / BOJ] acmicpc 1699 제곱수의 합 C++ (0) | 2022.05.01 |
| [백준/BOJ] acmicpc 1676 팩토리얼 0의 개수 (2) | 2021.11.16 |
